P1364 医院设置
题目描述
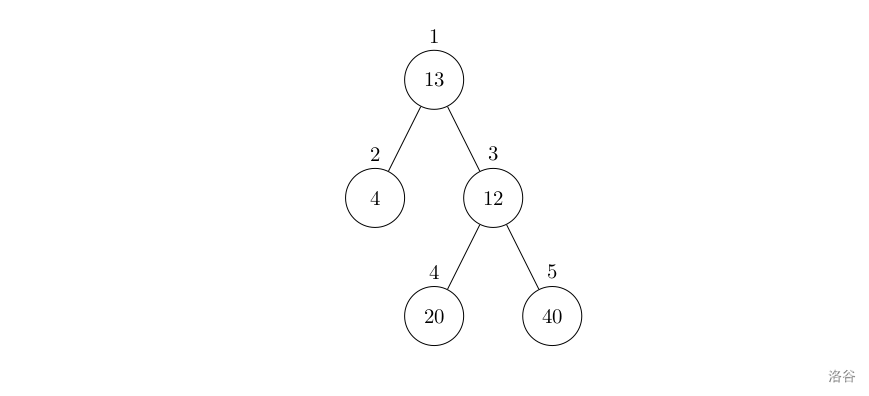
设有一棵二叉树,如图:

其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 $1$。如上图中,若医院建在 $1$ 处,则距离和 $=4+12+2\times20+2\times40=136$;若医院建在 $3$ 处,则距离和 $=4\times2+13+20+40=81$。
说明/提示
数据规模与约定
对于 $100%$ 的数据,保证 $1 \leq n \leq 100$,$0 \leq u, v \leq n$,$1 \leq w \leq 10^5$。
解题思路
初步分析
题目的意思是,圈中的数字表示节点中的人口,相邻接点之间的距离为 $1$。而寻求所有人口到达医院的最小距离之和。
思考问题
我们可以任意调整医院的位置,而医院的位置调整后,距离之和都会改变,而这种改变是有规律的。比如以图中医院节点由 $1$ 改成 $3$ 为例子,显而易见可以观察到,将会是 1节点所构成的树-节点3及子树的节点数量(将导致$3, 4, 5$集体上移) + 总数 - 节点3及子树(导致$3, 4, 5$外集体上移)。且时间复杂度在O(1)的情况。
那么我们该如何寻求母节点构成的树的最大值与节点与子树的数量呢?那么经过一次递归求答案,在递归中,将$ f(1)$的值求出,每一层的$ size(u) +=size(y)$ 即可得到 ,而后二次递归,树上dp求值,状态转移方程为$ f(y) = f(u)-size(y) + totol - size(y)$ 然后遍历求答案
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #include<bits/stdc++.h>
using namespace std ;
const int N = 1e3 ;
using ll = long long ;
struct Dim{
int w ;
int l ;
int r ;
};
Dim a[N] ;
ll sz[N] ;
ll dep[N] ;
ll size[N] ;
ll f[N] ;
ll ans = LONG_LONG_MAX ;
int totol ;
void dfs(int u, int dep_){
size[u] = a[u].w ;
dep[u] = dep_ ;
if(a[u].l != 0 ){
dfs(a[u].l , dep_ +1 );
size[u] +=size[a[u].l] ;
}
if(a[u].r != 0 ){
dfs(a[u].r , dep_ +1 );
size[u] +=size[a[u].r] ;
}
f[1]+=a[u].w *dep[u] ;
}
void dfs2(int u) {
if (a[u].l != 0) {
f[a[u].l] = f[u] - size[a[u].l] + (totol - size[a[u].l]);
dfs2(a[u].l);
}
if (a[u].r != 0) {
f[a[u].r] = f[u] - size[a[u].r] + (totol - size[a[u].r]);
dfs2(a[u].r);
}
}
void solve(){
int n ; cin >> n ;
for(int i= 1 ; i<= n ; i++){
cin>> a[i].w >>a[i].l >> a[i].r ;
}
dfs(1 , 0 ) ;
for(int i = 1 ; i<= n ; i++)totol +=a[i].w ;
dfs2(1 ) ;
for(int i = 1 ; i<= n ; i++){
ans = min(ans , f[i]);
}
cout << ans ;
}
int main() {
int t = 1 ;
while(t-- ){
solve();
}
return 0 ;
}
|